Does Finite Element Analysis need improvement?
Does Finite Element Analysis (FEA) need improvement or it is rock solid?
Introduction
When a young mechanical engineer starts his learning he is quickly taught that the mechanical world is divided into two binary halves. One half is rigid structures where the component parts do not move relative to other parts and that all reactions are local. FEA rules this world. The second half is the world of machines where parts do move in relationship to other parts. Dynamics, kinematics and tribology rule this world but FEA is not far away when it comes to analyzing each individual component of the machine as that component can be seen as a rigid structure in most cases (except for springs and hydraulic devices).
One Ring to Rule Them All
So is FEA the one ring rule to rule them all? Are there structures that do not fit in the neat categories above? If yes, are they worth studying to see if they can be analyzed by FEA, or does FEA need improvement to analyze them?
Tensegrities and Geodesic Domes (1)
Vigyan Ashram has been building geodesic domes ever since it was founded some 30 years ago. Many such domes were built by Vigyan Ashram after the earthquake that razed Latur as geodesic domes are considered earthquake-proof. But while the strength of geodesic domes has been seen in the structures that have been built and which have survived earthquakes and hurricanes, for a long time there was no comparison of the calculated strength of a dome versus the actual strength realized in the field. This might have been due to a few factors, including the fact that geodesic domes are far and few in number and the destructive testing of a dome was an expensive process. The fact that computing facilities to run FEA software were rare would also have played a role.
In 2009, Marek Kubik, then an engineering student at the Durham University School of Engineering, UK came to Vigyan Ashram to conduct an FEA analysis of the geodesic domes that Vigyan Ashram builds. Kubik's report, which he submitted as his engineering Master's thesis, contains many interesting ideas including how FEA Analysis can be conducted via a spread sheet. However the analysis, if substantially correct, only provides one half of the total test, i.e. it just gives the theoretical strength of the dome with no comparison with the actual strength.
FEA in its various avatars, has a century-old history. Thousands of rigid structures have been calculated and compared to actual engineered products and the results have tallied in a satisfactory manner when mesh size is made appropriate. So why doubt FEA results for geodesic domes?
Tensegrities and Geodesic Domes (2)
Tensegrities are a half-century old structures of which geodesic domes are a particular example.
All structures, properly understood, from the solar system to the atom, are tensegrity structures. Universe is omnitensional integrity. —R. Buckminster Fuller
I want to build a universe. —Kenneth Snelson
Tensegrity is a relatively new principle based on the use of isolated components in compression inside a net of continuous tension, in such a way that the compressed members (usually bars or struts) do not touch each other and the prestressed tensioned members (usually cables or tendons) delineate the system spatially. This dry definition of tensegrity does not make it easy to visualize a tensegrity structure. So here are two pictures of tensegrity structures, one simple and one complex:
 6-Strut Tensegrity, a stainless steel and steel wire sculpture by Buckminster Fuller, circa 1980. Size 14.25 in. x 17.25 in. x 15.75 in.
6-Strut Tensegrity, a stainless steel and steel wire sculpture by Buckminster Fuller, circa 1980. Size 14.25 in. x 17.25 in. x 15.75 in.
 Dragon, a stainless steel and steel wire tensegrity sculpture by Kenneth Snelson, circa 2000-03. Size 30.5 ft. x 31 ft. x 12 ft.
Dragon, a stainless steel and steel wire tensegrity sculpture by Kenneth Snelson, circa 2000-03. Size 30.5 ft. x 31 ft. x 12 ft.
References to various websites that give more photographs and other information on tensegrity structures are given in Appendix A.
Tensegrities and Geodesic Domes (3)
How do tensegrity structures differ from rigid bodies or machines that a new FEA is needed to be developed?
The first part of the answer below is reproduced from a 2004 thesis by Valentín Gómez Jáuregui at the School of Architecture, Queen’s University Belfast, UK (see section 4.5.1, page 82 of the thesis).
- They don’t depend on gravity due to their self-stability, so they don’t need to be anchored or leaned on any surface. The systems are stable in any position. The force of gravity, basis of the conventional architecture, is nullified (Perlberg, 1977)
- They have the property of synergy where the behavior of the whole systems is not predicted by the behavior of any of their components taken separately. (Fuller, 75; Levin, 82)
- They have the ability of respond as a whole, so local stresses are transmitted uniformly and absorbed throughout the structure.
- Elasticity multiplication is inherent to them: When separating two struts by a certain distance, the stretching of the tendons is much less than this amount. For example, in the expanded octahedron (fig.4.15) (Six strut tensegrity by Buckminster Fuller shown above), if the struts are separated by 1%, the tendons stretch 0.00166% (600 times less!), so the whole system has the capacity to multiply the elasticity of the tendon by 600 times. (Kenner, 1976). For an example, the deflection of the expanded octahedron modeled by cables and beams finite elements (Mijuca, 1997), can be seen in Appendix E.9 (Appended here also as Appendix B.)
- The response to the loads is non linear. They are more flexible under light loads, but their stiffness increases rapidly as the load is higher, like a suspension bridge (Kenner, 1976; Smaili, 2003; Wang 2003).
- Some tensegrities, under axial load, experience a rotation around this axis (Kenner, 1976; Snelson, 2004). The direction of this rotation depends on the handedness of the system.
A similar but more detailed description can be read on pages 11 to 16 of the book Geodesic Math and How to Use it by Hugh Kenner, partially available on-line through Google Books. On page 18 Kenner asserts that
It follows that calculations pertaining to such a system, taking into account the known characteristics of the materials but presuming the usual method of assembling them, are certain to be wrong. […] By analogy, the tensile network hidden in geodesic domes defeats all normal calculations of their strength.
FEA and Geodesic Domes
There are three known instances of FEA analysis of Geodesic Domes:
1. The FEA analysis of Pabal Type Geodesic Domes conducted by Marek Kubik. The work includes coordinates for various frequencies of geodesic domes. (Kubik, M.L., The Structural Analysis of Geodesic Domes. Engineering Masters Thesis, Durham University School of Engineering, April 2009.)
2. The FEA analysis of a dome’s hubs and struts by a mechanical engineering consultancy. (ASEMA International, Geodesic Dome Structural Analysis, Ballarat, Australia, April 2005.)
3. An ongoing comparative analysis of two alternate types of 3V and 4V geodesic domes being conducted by Peter Schwarzel. (CarbonWorks, Performance of domes using EMT tube, February 2017.)
Calculated Strength versus Realized Strength
Unfortunately all three analyses ignore the need to compare the theoretical calculations of strength with the actual realized strengths.
Hugh Kenner implies that the theoretical calculations will underestimate the strength by a factor of 300 to 600.
My own hunch is that FEA will underestimate the actual strength by a factor of 5 to 6. The need to compare the calculated results with actual realized strengths could not be more compelling when expected errors are of huge magnitudes.
Six Strut Tensegrity and Geodesic Domes
A six strut tensegrity has all the characteristics that a geodesic dome has hence it is an ideal candidate to theoretically calculate its strength for an actual model and to destructively test the model to determine its strength.
- A Six strut tensegrity is described on pages 11 to 16 of Hugh Kenner’s book Geodesic Math and How to Use it.
- A good introduction to tensegrities and how to build simple models is given here: http://www.tensegriteit.nl/e-simple.html
- A six strut tensegrity has six struts of identical lengths – call it unity or 1. It has 24 tendons of identical lengths – these are 0.612 times the strut length. If the struts are made from a EMT tube, a single length of 10 feet will provide the material for all the struts.
- Tendons can be cut from 16 gauge Galvanized Iron (G.I.) wire – even thinner 18 gauge G.I. wire will suffice. A roll of 30 feet in length will provide double the needed material.
- There are many videos on YouTube that give detailed instructions on how to make the six strut tensegrity, for example https://www.youtube.com/watch?v=8gtvxYZ0GIg.
The coordinates of a six strut tensegrity are calculated and given in Appendix A. Note the end results are given for both unit length strut and a 10 unit length strut. The calculations are followed by a image in png format that was generated from GeoGebra.
Appendix A: Cartesian Coordinates of Six Strut Tensegrities
Given:
- Let (0,0) be the center of the sphere on whose surface the end points of the six struts lie.
- Let the length of each strut be unity.
- Let the length of each tendon be 0.612.
- At equilibrium,the distance between two parallel struts can be shown to be 0.5.
Then:
- The radius of the sphere can be calculated as square root(0.25^2 +0.5^2) = 0.559016994.
- The pair AA’ and BB’ lie in (x,0,z) plane.
- The pair CC’ and DD’ lie in (x,y,0) plane.
- The pair EE’ and F F’ lie in (0,y,z) plane.
- The coordinates of six struts are as follows:
| Unit length Strut | 10 units length | |
|---|---|---|
| A coordinates | (0.25, 0, -0.5) | (2.5, 0, -5) |
| A’ coordinates | (0.25, 0, 0.5) | (2.5, 0, 5) |
| B coordinates | (-0.25, 0, -0.5) | (-2.5, 0, -5) |
| B’ coordinates | (-0.25, 0, 0.5) | (-2.5, 0, 5) |
| C coordinates | (0.5, 0.25, 0) | (5, 2.5, 0) |
| C’ coordinates | (-0.5, 0.25, 0) | (-5, 2.5, 0) |
| D coordinates | (0.5, -0.25, 0) | (5, -2.5, 0) |
| D’ coordinates | (-0.5, -0.25, 0) | (-5, -2.5, 0) |
| E coordinates | (0, -0.5, -0.25) | (0, -5, -2.5) |
| E’ coordinates | (0, 0.5, -0.25) | (0, 5, -2.5) |
| F coordinates | (0, -0.5, 0.25) | (0, -5, 2.5) |
| F’ coordinates | (0, 0.5, 0.25) | (0, 5, 2.5) |
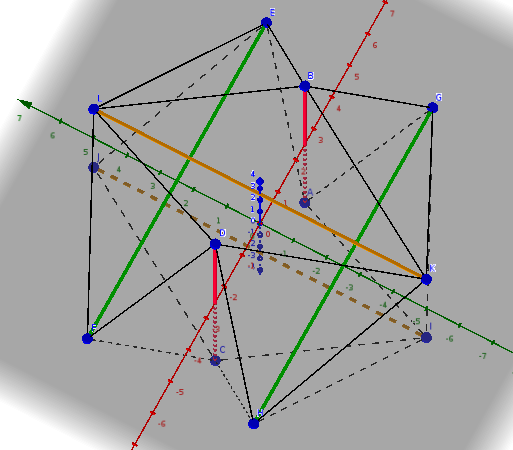 Six-strut tensigrity modeled in GeoGebra.
Six-strut tensigrity modeled in GeoGebra.
Appendix B: Tensegrity Structures and their Application to Architecture
Deflection of the expanded octahedron
In order to show the Elasticity Multiplication of tensegrity systems, the deflection of the expanded octahedron modeled by cables and beams finite elements (Mijuca, 1997), can be seen in next figures:
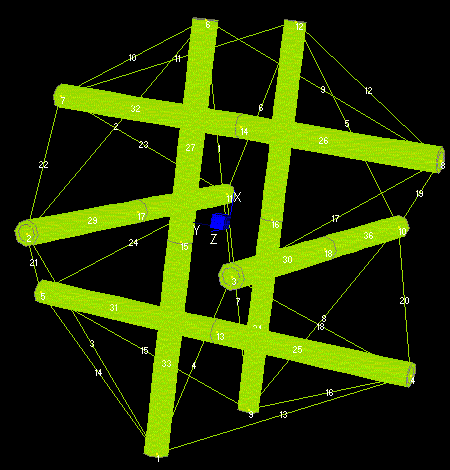 Fig. 1. Tensegrity, no deformation. Illustration taken from (Mijuca, 1997)
Fig. 1. Tensegrity, no deformation. Illustration taken from (Mijuca, 1997)
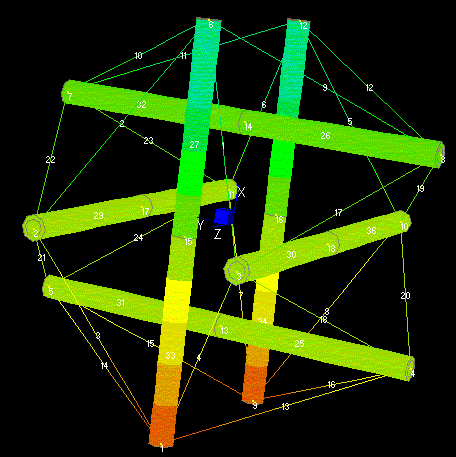 Fig. 2. Tensegrity, mid-deformation. Illustration taken from (Mijuca, 1997)
Fig. 2. Tensegrity, mid-deformation. Illustration taken from (Mijuca, 1997)
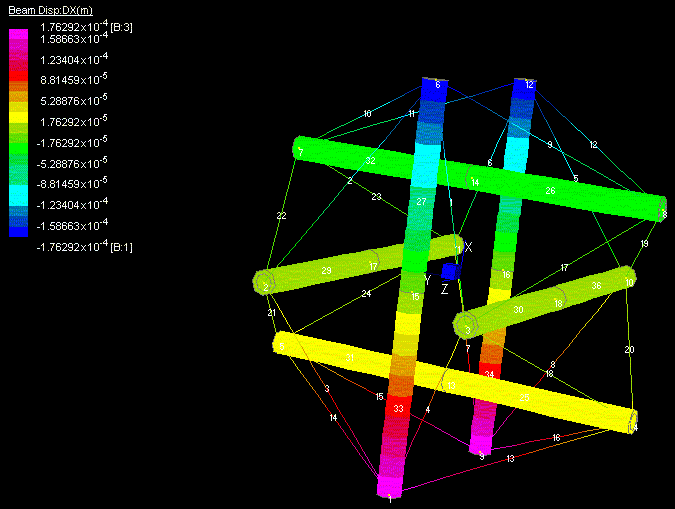 Fig. 3. Tensegrity, no deformation. Illustration taken from (Mijuca, 1997)
Fig. 3. Tensegrity, no deformation. Illustration taken from (Mijuca, 1997)